Congrats!

Function conducted by Kerala University to Felicitate Ph D awardees of the year 2012

Lagrange Bracket- K A Solaman

Lagrange Bracket

Let 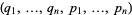 be any functions of two variables 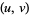. Then the expression

(1)

is called a Lagrange bracket (Lagrange 1808; Whittaker 1944, p. 298).

The Lagrange brackets are anticommutative,

(2)

(Plummer 1960, p. 136).

If 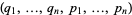 are any functions of  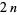variables 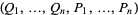, then

(3)

where the summation on the right-hand side is taken over all pairs of variables 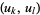 in the set .

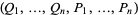But if the transformation from 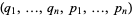 to 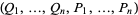 is a contact transformation, then

(4)

giving

			(5)
			(6)
			(7)
			(8)

Furthermore, these may be regarded as partial differential equations which must be satisfied by 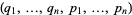, considered as function of  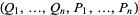in order that the transformation from one set of variables to the other may be a contact transformation.

Let 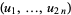 be 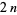 independent functions of the variables 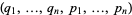. Then the Poisson bracket  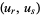is connected with the Lagrange bracket  by

(9)

where 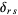 is the Kronecker delta. But this is precisely the condition that the determinants formed from them are reciprocal (Whittaker 1944, p. 300; Plummer 1960, p. 137).

SEE ALSO:

Quantum physicists win 2012 Physics Nobel prize

Like ·  · Share · 18 hours ago · 

STOCKHOLM: A French-American duo shared the 2012 Nobel Prize in physics on Tuesday for inventing methods to observe the properties of the quantum world, research that has led to the construction of extremely precise clocks and helped scientists take the first steps toward building superfast computers.
Serge Haroche of France and American David Wineland opened the door to new experiments in quantum physics by showing how to observe individual quantum particles while preserving their quantum properties.
A quantum particle is one that is isolated from everything else. In this situation, an atom or electron or photon takes on strange properties. It can be in two places at once, for example. It behaves in some ways like a wave. But these properties are instantly changed when it interacts with something else, such as when somebody observes it.
Working separately, the two scientists, both 68, developed "ingenious laboratory methods" that allowed them to manage and measure and control fragile quantum states, the Royal Swedish Academy of Sciences said.
"Their ground-breaking methods have enabled this field of research to take the very first steps towards building a new type of superfast computer based on quantum physics," the academysaid. "The research has also led to the construction of extremely precise clocks that could become the future basis for a new standard of time."
Haroche is a professor at the College de France and Ecole Normale Superieure in Paris. Wineland is a physicist at the National Institute of Standards and Technology, or NIST, and the University of Colorado in Boulder, Colorado. The two researchers use opposite approaches to examine, control and count quantum particles, the academy said. Wineland traps ions - electrically charged atoms - and measures them with light, while Haroche controls and measures photons, or light particles.
Haroche said he was out walking with his wife when he got the call from Nobel judges. "I was in the street and passing a bench so I was able to sit down," Haroche told a news conference inStockholm by phone. "It's very overwhelming." He said his work in the realm of quantum physics could ultimately lead to unimaginably fast computers.

ഭൌതിക ശാസ്ത്രത്തിനുള്ള നൊബെല്‍ സെര്‍ജെയും വിന്‍ഫീല്‍ഡും പങ്കിട്ടു

സ്റ്റോഖ്‌ഹോം: പ്രകാശത്തിന്റെ അടിസ്ഥാന ഘടകങ്ങളായ ഫോട്ടോണുകളെ കുറിച്ചുള്ള പഠനം നടത്തിയ ശാസ്ത്രജ്ഞര്‍ക്ക് ഭൗതികശാസ്ത്രത്തിനുള്ള ഈ വര്‍ഷത്തെ നോബല്‍ സമ്മാനം ലഭിച്ചു. ഫ്രഞ്ചുകാരനായ സെര്‍ജെ ഹരോഷെ അമേരിക്കക്കാരനായ ഡേവിഡ് വിന്‍ഫീല്‍ഡ് എന്നിവര്‍ക്കാണ് നോബല്‍. രണ്ടു പേര്‍ക്കും 1.2 മില്യണ്‍ ഡോളര്‍ വീതം ലഭിക്കും.

ക്വാണ്ടം ഒപ്റ്റിക്സിന്റെ പഠനത്തില്‍ ഇരുവരും പുതിയ വാതായനങ്ങള്‍ തുറന്നതായി റോയല്‍ സ്വീഡിഷ്‌ അക്കാദമി വാര്‍ത്താക്കുറിപ്പില്‍ വ്യക്തമാക്കി. സ്വതന്ത്രമായ ഊര്‍ജകണങ്ങളെ അവയെ നശിപ്പിക്കാതെ തന്നെ കണ്ടെത്തുന്ന പരീക്ഷണമാണ്‌ ഇരുവരും നടത്തിയത്‌.

ഗവേഷകര്‍ നേരത്തെ അസാധ്യമെന്ന്‌ വിധിയെഴുതിയ കാര്യമായിരുന്നു ഇത്‌. പുതിയ സൂപ്പര്‍ ഫാസ്റ്റ്‌ കംപ്യൂട്ടറുകള്‍ പോലും നിര്‍മിക്കാന്‍ സഹായകമാകുന്ന കണ്ടുപിടുത്തമാണ്‌ ഇവരുടേത്‌.

Comment: Fascinating Physics!

-K A Solaman