Tuesday, October 23, 2012

Lagrange Bracket- K A Solaman


Lagrange Bracket

Contribute to this entry
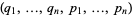Let (q_1,...,q_n,p_1,...,p_n) be any functions of two variables 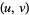(u,v). Then the expression
[u,v]=sum_(r=1)^n((partialq_r)/(partialu)(partialp_r)/(partialv)-(partialp_r)/(partialu)(partialq_r)/(partialv))
(1)
is called a Lagrange bracket (Lagrange 1808; Whittaker 1944, p. 298).
The Lagrange brackets are anticommutative,
[u_l,u_m]=-[u_m,u_l]
(2)
(Plummer 1960, p. 136).
If 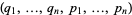(q_1,...,q_n,p_1,...,p_n) are any functions of 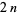2n variables 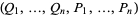(Q_1,...,Q_n,P_1,...,P_n), then
sum_(r=1)^n(dp_rdeltaq_r-deltap_rdq_r)=sum_(k,l)[u_k,u_l](du_ldeltau_k-deltau_ldu_k),
(3)
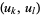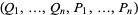where the summation on the right-hand side is taken over all pairs of variables (u_k,u_l) in the set (Q_1,...,Q_n,P_1,...,P_n).
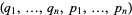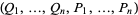But if the transformation from (q_1,...,q_n,p_1,...,p_n) to (Q_1,...,Q_n,P_1,...,P_n) is a contact transformation, then
sum_(r=1)^n(dp_rdeltaq_r-deltap_rdq_r)=sum_(r=1)^n(dP_rdeltaQ_r-deltaP_rdQ_r),
(4)
giving
[P_i,P_k]=0 for i,k=1,2,...,n
(5)
[Q_i,Q_k]=0 for i,k=1,2,...,n
(6)
[Q_i,P_k]=0 for i,k=1,2,...,n,i!=k
(7)
[Q_i,P_i]=0 for i=1,2,...,n.
(8)
Furthermore, these may be regarded as partial differential equations which must be satisfied by 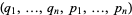(q_1,...,q_n,p_1,...,p_n), considered as function of 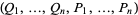(Q_1,...,Q_n,P_1,...,P_n) in order that the transformation from one set of variables to the other may be a contact transformation.
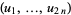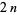Let (u_1,...,u_(2n)) be 2n independent functions of the variables 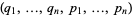(q_1,...,q_n,p_1,...,p_n). Then the Poisson bracket 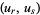(u_r,u_s) is connected with the Lagrange bracket [u_r,u_s] by
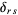sum_(t=1)^(2n)(u_t,u_r)[u_t,u_s]=delta_(rs),
(9)
where delta_(rs) is the Kronecker delta. But this is precisely the condition that the determinants formed from them are reciprocal (Whittaker 1944, p. 300; Plummer 1960, p. 137).
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)